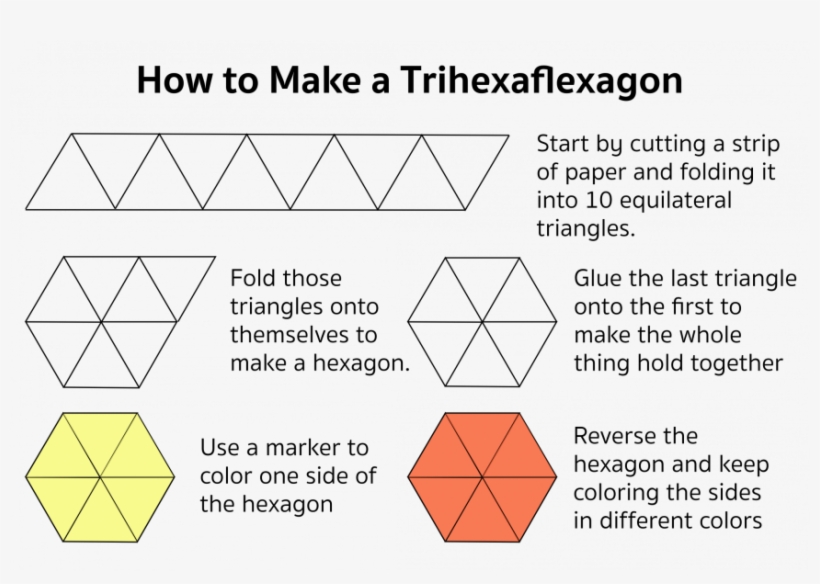
FLEXAGONS are paper polygons, folded from straight or crooked strips of paper, which have the fascinating property of changing their faces when they are “flexed.” Had it not been for the trivial circumstance that British and American notebook paper are not the same size, flexagons might still be undiscovered, and a number of top-flight mathematicians would have been denied the pleasure of analyzing their curious structures.
It all began in the fall of 1939. Arthur H. Stone, a 23- year-old graduate student from England, in residence at Princeton University on a mathematics fellowship, had just trimmed an inch from his American notebook sheets to make them fit his English binder. For amusement he began to fold the trimmed-off strips of paper in various ways, and one of the figures he made turned out to be particularly intriguing. He had folded the strip diagonally at three places and joined the ends so that it made a hexagon [seeFig.I]. When he pinched two adjacent triangles together and pushed the op- posite corner of the hexagon toward the center, the hexagon would open out again, like a budding flower, and show a completely new face. If, for instance, the top and bottom faces of the original hexagon were painted different colors, the new face would come up blank and one of the colored faces would disappear !
This structure, the first flexagon to be discovered, has three faces. Stone did some thinking about it overnight, and on the following day confirmed his belief (arrived at by pure cerebration) that a more complicated hexagonal model could be folded with six faces instead of only three. At this point Stone found the structure so interesting that he showed his paper models to friends in the graduate school. Soon “flex-agons” were appearing in profusion at the lunch and dinner tables. A “Flexagon Committee” was organized to probe further into the mysteries of flexigation. The other members besides Stone were Bryant Tuckerman, a graduate student of mathematics ; Richard P. Feynman, a graduate student in physics; and John W. Tukey, a young mathematics instructor.
The models were named hexaflexagons- “hexa” for their hexagonal form, and “flexagon” for their ability to flex. Stone’s first model is a trihexaflexagon (“tri” for the three different faces that can be brought into view) ; his elegant second structure is a hexahexaflexagon (for its six faces).